Apriori与FP-Growth算法的实现与比较

发表于 | 阅读次数:

本文是哈工大2017年秋季《数据挖掘理论与算法》课程实验第一大题的实验报告。

主要实现了Apriori算法和FP-Growth算法并对他们做了时间、内存性能上的比较。

实验说明书和源代码参见GitHub Repo。实验要求也可以见于每一小节的开头。

Algorithm Implementation

(a) Describe your implementation. If open-source software is referenced, please acknowledge the authors of the software.

In this project we use Python to implement two different frequent itemset mining algorithms Apriori and FP-Growth. The basic principle of two algorithms are already introduced in the class. Therefore, we just introduce the basic steps here.

Machine Learning in Action is the only reference source. We didn’t copy the code but write it again to make them more clear and understandable.

Hardware/Software Configuration

  • Hardware
  • CPU: Intel(R) Xeon(R) CPU E5-2678 v3 @ 2.50GHz
  • Core Number: 48
  • Memory: 60G
  • Software
  • Ubuntu 14.04 LTS
  • Python 3.5

Apriori

Apriori Principle: The non-empty subsets of a frequent itemset is frequent, which means, the supersets of a infrequent itemset is also infrequent.

  • Candidate generate
  • Candidate pruning

The framework / basic APIs of the code is as below, I do the comment to explain the usage of each method. To see the complete code please refer to the appendix.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
def candidate_initialize(transaction_database):  # Generate 1-size candidates (items)
def support_counting(transaction_database, itemset_list):  # Scan the database and count the support.
def candidate_generate(itemset_list, k):  # Generate k-size candidates in the k-th step. (Combine F_{k-1}xF_{k-1})
def candidate_pruning(transaction_database, candidate_itemset_list, minsup):  # Given the candidates, pruning all infrequent itemsets.
def apriori(transaction_database, minsup=0.5):  # The main Apriori algorithm.
def display(frequent_itemset_list, support):  # To visualize the result.
def main():
    parser = argparse.ArgumentParser()  # Define the hyper-parameters.
    parser.add_argument('--ntrans', type=float, default=1)
    parser.add_argument('--tlen', type=int, default=10)
    parser.add_argument('--nitems', type=float, default=1)
    parser.add_argument('--minsup', type=float, default=0.5)
    args = parser.parse_args()
    transaction_database = load_ibm_dataset(args.ntrans, args.tlen, args.nitems,
                                            args.npats, args.patlen)
    frequent_itemset_list, support = apriori(transaction_database, args.minsup)
if __name__ == '__main__':
    main()

FP Growth

FP Growth algorithm applies the Apriori Principle too, instead, it build a FP Tree in the beginning. This data structure helps it to mine the frequent itemsets more effectively.

  • Build the FP tree and the header table.
  • Recursively generate the conditional pattern bases.
  • Mining the tree

The framework / basic APIs of the code is as below, I do the comment to explain the usage of each method. To see the complete code please refer to the appendix.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class TreeNode(object):  # The basic component in the FP-Tree structure.
def create_tree(transaction_database, minsup):
def update_tree(ordered_itemset, fp_tree, header_table):
def update_header(initial_node, target_node):
def ascend_tree(leaf_node, prefix_path):  # Given a item, backtrack the tree and record the nodes in the path.
def find_prefix_path(item, header_table):  # Given a item, find all prefix paths (which are also call conditional pattern bases).
def mine_tree(fp_tree, header_table, minsup,frequent_itemset=set([]), frequent_itemset_list=[], support_count_list=[]):  # Recursively apply this method to find the frequent items and the itemsets contain them.
def display(transaction_database, frequent_itemset_list, support_count_list):  # To visualize the result.
def main():
    parser = argparse.ArgumentParser()
    parser.add_argument('--ntrans', type=int, default=1)
    parser.add_argument('--tlen', type=int, default=10)
    parser.add_argument('--nitems', type=int, default=1)
    parser.add_argument('--minsup', type=float, default=0.5)
    args = parser.parse_args()
    args.minsup *= args.ntrans * 1000
    transaction_database = load_ibm_dataset(args.ntrans, args.tlen, args.nitems,
                                            args.npats, args.patlen)
    fp_tree, header_table = create_tree(transaction_database, args.minsup)
    frequent_itemset_list, support_count_list = mine_tree(fp_tree, header_table, args.minsup)
if __name__ == '__main__':
    main()

Verification

We construct a toy transaction dataset to verify whether the programs are implemented correctly. The toy dataset is derived from the handout given by Prof. Zou in class.

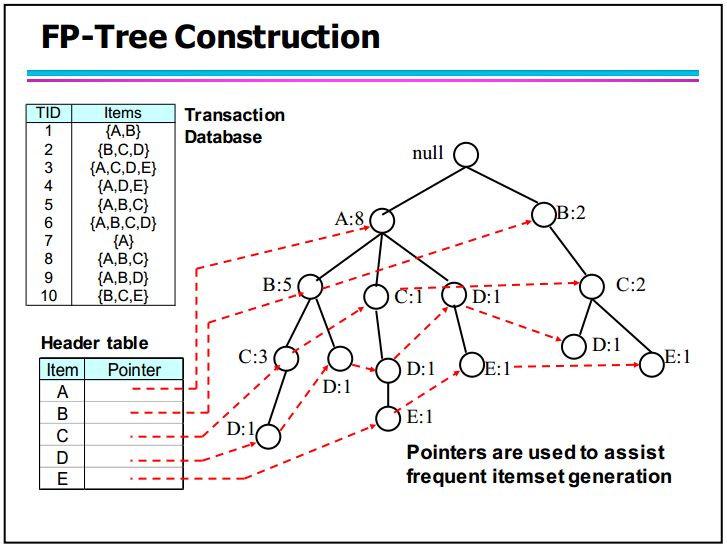
The result of Apriori algorithm is as below:

1
2
3
4
5
6
7
8
9
$ python apriori.py --minsup=0.5
{'B'} 				 0.7
{'A'} 				 0.8
{'D'} 				 0.5
{'C'} 				 0.6
{'B', 'A'} 			 0.5
{'B', 'C'} 			 0.5
Total 6 frequent itemsets.

The result of FP Growth algorithm is as below: (with a visualized FP Tree)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
$ python fp_growth.py --minsup=0.5
[FP Tree]
  null   1
   A   8
    B   5
     C   3
      D   1
     D   1
    C   1
     D   1
      E   1
    D   1
     E   1
   B   2
    C   2
     D   1
     E   1
{'A'} 			 0.8
{'B'} 			 0.7
{'B', 'A'} 			 0.5
{'C'} 			 0.6
{'B', 'C'} 			 0.5
{'D'} 			 0.5
Total 6 frequent itemsets.

The results indicate the correctness of our implementation.

Parallel Programming

Since this experiment requires lots of results to observe the impact of several parameters, running the programs one by one may looks clumsy and wastes lots of time. We run our algorithm on a multi-CPU server in parallel. On this point we use a Pythonic way to run our programs in parallel automatically.

In Python,we can uses a class named multiprocessing.Pool to run multiple command on multiple CPU cores in parallel.

1
2
pool = multiprocessing.Pool(multiprocessing.cpu_count())
pool.map(os.system, cmd_list)

We need to write all bash commands (like python apriori.py with different parameters) in cmd_list (in form of strings). Instance pool will assign each task to a core then os.system will execute each command. In this way, we can run 48 experiment at the same time and save lots of time!

Datasets Generation

(b) Generate synthetic datasets using the IBM Synthetic Data Generator for Itemsets and Sequences available at https://github.com/zakimjz/IBMGenerator.

In order to fine-tune the parameters we need a more complicated dataset generator rather than some toy datasets. We use the IBM Synthetic Data Generator to generate the Itemsets.

Use the bash commands below to download and compile the tool.

1
2
3
$ git clone git@github.com:zakimjz/IBMGenerator.git
$ cd IBMGenerator
$ make

Use the bash commands below to generate a toy dataset.

1
$ ./gen lit -ntrans 100 -tlen 10 -nitems 1 -npats 1000 -patlen 4 -fname T10I4D100K -ascii

Where -ntrans controls the number of transactions, -tlen controls the length of transactions, -nitems controls the number of distinct items. These three arguments are important to us since we need to fine tune them to observe the performance of the algorithms.

Use the bash commands below to view the dataset.

1
2
3
4
5
6
7
8
9
10
11
12
13
$ less T10I4D100K.data
1 1 7 492 536 586 589 681 861 959
2 2 7 190 279 541 773 797 801 878
3 3 3 135 608 876
4 4 16 19 301 318 364 492 493 586 681 742 797 828 831 861 892 916 959
5 5 13 66 117 202 388 395 416 419 501 712 741 783 844 989
...
99995 99995 5 19 269 755 831 992
99996 99996 7 78 189 190 241 650 751 882
99997 99997 9 113 190 275 395 449 592 781 797 936
99998 99998 13 43 338 364 456 501 614 709 862 888 905 950 951 959
99999 99999 11 75 101 187 218 221 286 295 562 774 792 925
100000 100000 17 34 244 261 330 336 396 401 492 521 531 586 617 646 681 861 952 959

The 1st column is CustID, 2nd column is TransID, 3rd column is NumItems and the rests are Items. (We only use the Items data.)

Here we encapsulate this data generator into a Python function, which generate the IBM format data and convert to the data that Python can read, like this:

1
[{492, 536, 586, 589, 681, 861, 959}, {190, 279, 541, 773, 797, 801, 878}, ...]

Parameters Fine-tuning

(c) Test the impact of the following parameters on the performance (e.g., running time and memory comsumption) of the algorithms.

• The minimum support threshold minsup

• The number of transactions

• The length of transactions

• The number of distinct items

In this Chapter we will use IBM Synthetic Data Generator and the algorithms we implemented, to fine-tune 4 kinds of parameters as required in the

Tools & Evaluation Metrics

In order to collect the information of time and memory consumed by the algorithms, we introduce a Pythonic way to measure them. we use two powerful tools line_profiler and memory_profiler. In order to install them, just type

1
pip install line_profiler psutil memory_profiler

Then insert decorator @profile before the methods we interest in in the code, like this

1
2
@profile
def apriori(transaction_database, minsup=0.5):

Then run your code in this way if you want to observe the consumed time:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
$ kernprof -lv apriori.py
Total time: 309.309 s
File: apriori.py
Function: apriori at line 48
Line # Hits     Time  Per Hit  % Time   Line Contents
========================================================
48                                      @profile
49                                      def apriori(transaction_database, minsup=0.5):
50     1     1106016  1106016    0.4      candidate_1 = candidate_initialize(...)
53     1     8153210  8153210    2.6      pruned_1, support = candidate_pruning(...)      
54     1           3      3.0    0.0      frequent_itemset_list = [pruned_1]
55     1           1      1.0    0.0      k = 2
56    12          26      2.2    0.0      while(len(frequent_itemset_list[k-2]) > 0):
57    11     4280304 389118.5    1.4          candidate_k = candidate_generate(...)
58    11   295767919 26887992   95.6          pruned_k, support_k = candidate_pruning(..
61    11        1092     99.3    0.0          support.update(support_k)
62    11          44      4.0    0.0          frequent_itemset_list.append(pruned_k)
63    11          10      0.9    0.0          k += 1
64     1           0      0.0    0.0      return frequent_itemset_list, support

… and in this way if you want to observe the consumed memory:

1
2
3
4
5
6
7
8
9
$ python -m memory_profiler apriori.py
Filename: apriori.py
Line #    Mem usage    Increment   Line Contents
================================================
    86   35.418 MiB    0.000 MiB   @profile
    87                             def main():
    88   36.414 MiB    0.996 MiB       transaction_database = load_ibm_dataset(ntrans, ...
    89   36.652 MiB    0.238 MiB       apriori(transaction_database, minsup)

In this way we can observe the consumed time and memory line by line. We will soon use this tool to collect the data we need.

☆☆☆ Notice that: Using the line_profiler and memory_profiler will increase the total running time (roughly x1 to x5). The more decorator @profile you add before methods, the slower the program.

Experiment Design

The parameters we set are as follows:

  • Default:

ntrans=5(k), tlen=10, nitems=1(k), minsup=0.02

Fine-tune one of the parameter and keep other 3 default. The fine-tuned parameters are set as follows:

  • number of transactions(ntrans):

[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20] (Unit: k)

  • length of transaction(tlen):

[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20]

  • number of items(nitems):

[0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0, 1.1, 1.2, 1.3, 1.4, 1.5, 1.6, 1.7, 1.8, 1.9, 2.0] (Unit: k)

  • minimal support threshold(minsup):

[0.01, 0.02, 0.03, 0.04, 0.05, 0.06, 0.07, 0.08, 0.09, 0.1, 0.11, 0.12, 0.13, 0.14, 0.15, 0.16, 0.17, 0.18 , 0.19, 0.2]

In this way, we derive 20x4=80 results. We draw four line charts for each fine-tuned parameter as follows:

Time Performance

Notice that:

  • The red full line represents Apriori, the blue dash line represents FP Growth.
  • The real time should divide by roughly 3, since the line_profiler will make the program slower roughly x1~x5.

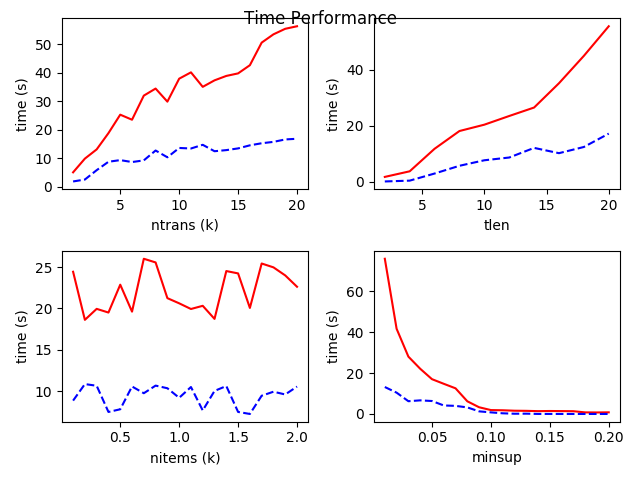
The figures indicate that:

  • Basically, FP Growth algorithm is better than Apriori algorithm at most time. It is because FP Growth pre-construct a FP Tree data structure to store the item more “tightly”, which facilitate mining.
  • With number of transactions(ntrans) increasing, both Apriori and FP Growth cost more time. But Apriori cost far more time than FP Growth.
  • The length of transaction(tlen) behaves just like the ntrans.
  • The variation of the number of items(nitems) seems impact less on the time performance.
  • With the minimal support threshold(minsup) increasing, both algorithms run faster and their performance become alike. It is because Apriori is able to prune most of candidate itemsets at each step and converges quickly. So, if we want a shorter running time, just make this parameter smaller.

Space/Memory Performance

Notice that:

  • The red full line represents Apriori, the blue dash line represents FP Growth.

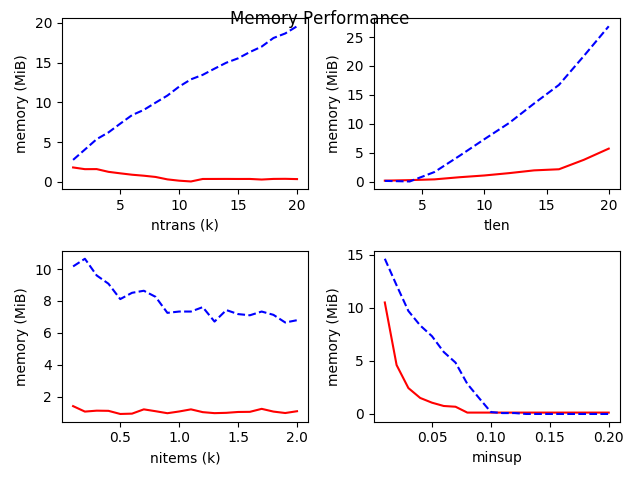
The figures indicate that:

  • Basically, the FP Growth takes more memory than Apriori. It is because of not only the pre-construction of FP Tree, but also the recursive construction of conditional FP Tree (the mining procedure).
  • With the number of transactions(ntrans) increasing, FP Growth’s memory consumption increases linearly. But Apriori’s memory consumption stays steady.
  • With the length of transaction(tlen) increasing, both Apriori and FP Growth consume more memory.
  • The variation of the number of items(nitems) seems impact less on the memory performance.
  • With the minimal support threshold(minsup) increasing, both algorithms consume less memory and their performance become alike.

Detailed Time Analysis

(d) Test the running time taken by each major procedure of the algorithms, for example, candidate generation, candidate pruning, and support counting of the Apriori algorithm.

In this Chapter we still use the powerful tool line_profiler to analyze the running time taken by each major procedure of the algorithms. The content of log files are shown in 3.1 Tools & Evaluation Metrics so we won’t explain again.

Since different parameters result in different performance, we randomly sample several of them to analyze.

Notice that:

  • the absolute value of time may be meaningless due to the different parameters. We should take focus on their proportion (%) in the whole run time of algorithm.
  • The whole run time of the algorithm doesn’t include the time to pre-process the dataset.

Apriori

There are three major procedures in Apriori, “support counting”, “candidate generation” and “candidate pruning”.

Notice that:

  • “support counting” is part of “candidate pruning”.
parameters support counting (μs) % candidate generation (μs) % candidate pruning (μs) %
1k, 10, 1k, 0.05 3868041 81.50 868597 18.30 3877056 81.68
5k, 10, 1k, 0.05 23639936 94.46 1376908 5.50 23649498 94.49
5k, 20, 1k, 0.05 45091836 91.55 4144611 8.41 45108920 91.58
5k, 10, 0.1k, 0.05 24750085 93.99 1557087 5.91 24775948 94.08
5k, 10, 1k, 0.20 786266 71.57 311974 28.40 786564 71.60

The table above indicates that:

  • “Support counting” takes nearly almost all time in the “candidate pruning”. Because each time the Apriori does the pruning operation, it need to scan the whole transaction database and count the support of the itemsets.
  • In most cases, “candidate pruning” takes far more time than “candidate generation”.

FP Growth

There are three major procedures in FP Growth, “create tree”, “find prefix path” and “mine tree”.

Notice that:

  • “create tree” means creating the first and complete FP Tree, not conditional FP Tree, which is part of “mine tree”.
  • “find prefix” is part of “mine tree”.
parameters create tree (μs) % find prefix path (μs) % mine tree (μs) %
1k, 10, 1k, 0.05 215754 11.93 123851 6.85 1593375 88.07
5k, 10, 1k, 0.05 3185766 25.52 409409 3.28 9299374 74.48
5k, 20, 1k, 0.05 14591858 44.46 1242425 3.78 18226332 55.54
5k, 10, 0.1k, 0.05 6988338 41.62 540334 3.22 9802346 58.38
5k, 10, 1k, 0.20 252681 96.99 182 0.07 7829 3.01

The table above indicates that:

  • FP Growth takes a long time (usually 10%-50%) to build a FP Tree before mining, which helps it save more time in the mining procedure.
  • When minsup is large, building a FP Tree, in fact, is not necessary. Due to this, the Apriori performs well in this situation.

Reference

  • Machine Learning in Action, Peter Harrington
    • Notice that the code in Chapter 12 Efficiently finding frequent itemsets with FP-growth has some bugs, which make the tree built incorrectly.