基于HMM模型的词性标注器Python实现

发表于 | 阅读次数:

说明

  • 本文代码对应Graham Neubig的nlptutorial系列中的第四讲Part of Speech Tagging with Hidden Markov Models，主要讲解用隐马尔科夫模型（Hidden Markov Model，HMM）实现一个词性标注器。

  • 对应Slides位于此处。

  • 本文的示例代码位于此处。

  • 依赖
    • Python3
    • numpy

  • 建议在阅读代码（5 HMM 训练~8 HMM 测试（维特比算法）小节）之前，至少需要过一遍简单的真实例子（4 HMM 真实例子小节），知道代码在干什么。也建议快速读一下基础部分（1 生成式模型基础和2 HMM 基础），该部分既不严谨也不全面，但对于阅读代码而言足够。

生成式模型基础

  • \(x = x_1, x_2, ..., x_n\) 观察变量，本文中可以视为单词序列。

  • \(y = y_1, y_2, ..., y_n\) 隐变量（状态变量），本文中可以视为词性序列。

  • 问题：给定\(x\)，如何求各种\(y\)的可能性（即\(P(y|x)\)）？或者说，如何求最大可能性的\(y\)（即\(y=argmax_y P(y|x)\)）？

  • 有两种方法：
    • 一种方法是直接对\(P(y|x)\)建模。叫做判别式模型（discrimitive model）；
    • 另一种方法则迂回一下，将\(P(y|x)\)转化为\(P(y|x)=\frac{P(x, y)}{P(x)}\)来求解。又因为\(P(x, y)\)一般特别难以完全求解，因为 \[ \begin{align*} P(x, y) &= P(x_1, x_2, ..., x_n, y_1, y_2, ..., y_n) \\ &= P(x_1)\cdot P(x_2|x_1)\cdot P(x_3|x_1, x_2)\cdot...\cdot \\ & P(y_1|x_1, x_2, ..., x_n)\cdot P(y_2|x_1, x_2, ..., x_n, y_1)\cdot...\cdot \\ & P(y_n|x_1, x_2, ..., x_n, y_1, y_2, ..., y_{n-1}) \end{align*} \] HMM模型和其他一些生成式模型都是在想方设法简化该项的分解形式。一般进一步转化为 \(P(y|x)=\frac{P(x|y)P(y)}{P(x)}\)。叫做生成式模型（generative model）。之所以叫这个名字，大概是因为这个公式中含有\(P(x|y)\)，这个意思是给定标签“生成”数据。一般来说标签数量较少（比如只有几十种词性），而数据是千变万化的（比如有成千上万的单词），“少”的标签去生成“多”的数据，是谓生成。

  • 大部分情况下我们是已知\(x\)，只需求最有可能的\(y\)，而无需求所有可能的\(y\)的分布。即：\[y=argmax_y P(y|x) = argmax_y \frac{P(x|y)P(y)}{P(x)}\] 因为分母和所求参数\(y\)无关，因此可以不用求\(P(x)\)，省去大量计算。即： \[y=argmax_y P(y|x) = argmax_y P(x|y)P(y)\] （注：这种方法有个术语。在贝叶斯学派的观念中，参数和变量没有区别，所以可以将变量\(y\)视为参数来做估计。这里描述的这种不求完整分布，只需要求能达到最大概率的参数值的方法，在参数估计中叫做最大后验概率估计（Maximum A Posteriori，MAP）。）

HMM 基础

  • HMM将公式\(y=argmax_y P(y|x) = argmax_y P(x|y)P(y)\)进一步拆解。

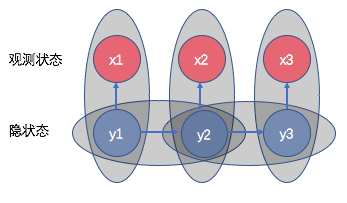
    上图中一个灰色椭圆代表一个条件概率。

  • 通过独立输出假设：每一个观测变量状态跟且仅跟其隐变量状态相关。简化下式： \[P(x|y)=P(x_1,x_2,...,x_n|y_1, y_2, ..., y_n)=P(x_1|y_1)P(x_2|y_2)...P(x_n|y_n)\]

  • 通过马尔可夫假设：后一状态只与前一状态有关。简化下式： \[P(y)=P(y_1, y_2, ..., y_n)=P(y_1|<s>)P(y_2|y_1)...P(</s>|y_n)\] （<s>和</s>表示句子首尾）

  • 所以： \[ \begin{align*} y &= argmax_y P(y|x) = argmax_y P(x|y)P(y) \\ &= argmax_{y_1, y_2, ..., y_n} \prod_i^n P(x_i | y_i) \prod_i^n P(y_i|y_{i-1}) \end{align*} \]

HMM 真实例子

  • \(x = 你, 很, 美\)

  • \(y = 代词, 副词, 形容词\) （可能的词性序列之一）

  • HMM 的图示如下：

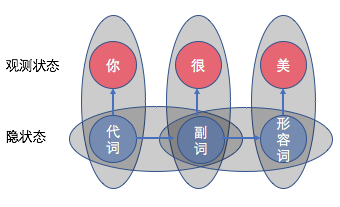
  • 我们问题是：已知\(x = 你, 很, 美\)，计算该序列对应的词性序列为\(y = 代词, 副词, 形容词\)的概率。

  • 由前面的计算公式可知： \[ \begin{align*} y &= argmax_y P(y|x) = argmax_y \frac{P(x, y)}{P(x)} \\ &= argmax_y P(x, y) = argmax_y P(x|y)P(y) \\ &= argmax_{y_1, y_2, ..., y_n} \prod_i^n P(x_i | y_i) \prod_i^n P(y_i|y_{i-1}) \end{align*} \] 这里\(y\)有多种可能，这里以\(y = 代词, 副词, 形容词\)为例，计算\(argmax\)内部的\(P(x, y)\)： \[ \begin{align*} P(x, y) &= P(你, 很, 美, <s>, 代词, 副词, 形容词, </s>) \\ &= P(你, 很, 美|<s>, 代词, 副词, 形容词, </s>) \cdot \\ & P(<s>, 代词, 副词, 形容词, </s>) \\ &= [P(你|代词)P(很|副词)P(美|形容词)]\cdot \\ & [P(代词|<s>)P(副词|代词)P(形容词|副词)P(</s>|形容词)] \end{align*} \] 我们要求出每种可能的\(y\)序列的\(P(x, y)\)值，然后取让其最大的\(y\)序列（即\(argmax_{y_1, y_2, ..., y_n}\)）。 在按照这样计算每一个\(y\)序列之后，取值最大的，返回对应的\(y\)序列，就是我们认为正确的词性。

  • “\(P(你|代词)P(很|副词)P(美|形容词)\)”叫做发射概率（emission probability），字面意思是从一个词性中发射/生成出某一个单词的概率。比如\(P(你|代词)\)表示从这么多代词中选一个对应的单词，这个单词为“你”的可能性是多少。

  • “\(P(代词|<s>)P(副词|代词)P(形容词|副词)P(</s>|形容词)\)”叫做转移概率（transition probability），表示从一个词性转移到下一个词性的概率。比如\(P(副词|代词)\)表示上一个词的词性是代词，那么下一个词的词性是副词的概率是多少。

  • 发射概率和转移概率都可以从标注文档中通过统计得到。

  • HMM 主要分为两部分：训练和解码。分别对应本文档中的5 HMM 训练和8 HMM 测试（维特比算法）。对应代码中的train_hmm.py和test_hmm.py。

  • 最后要注意一点是：上面的概率有的值很小，相乘后就更小了，限于计算机的精度，相乘容易造成下溢。一般我们会使用log来将相乘变为相加。如果使用对数（log）进行处理，则依旧是求\(argmax\)；如果使用负对数（-log）进行处理，则改为求\(argmin\)。Neubig的Slides中取了负对数，因此我们实验中也取负对数。

HMM 训练

  • train_hmm.py的 API 和 main 函数： 

    1
    2
    3
    4
    5
    6
    7
    8
    9
    def train_hmm(training_file, model_file):  # 总函数。
    if __name__ == '__main__':
        parser = argparse.ArgumentParser()  # 定义命令行传入参数。
        parser.add_argument('--training-file', type=str)
        parser.add_argument('--model-file', type=str, default='stdout')
        args = parser.parse_args()
        train_hmm(args.training_file, args.model_file)

  • 输入文件（标注语料）： 

    1
    2
    3
    $ less data/wiki-en-train.norm_pos
    Natural_JJ language_NN processing_NN -LRB-_-LRB- NLP_NN -RRB-_-RRB- is_VBZ a_DT field_NN of_IN computer_NN science_NN ,_, artificial_JJ intelligence_NN -LRB-_-LRB- also_RB called_VBN machine_NN learning_NN -RRB-_-RRB- ,_, and_CC linguistics_NNS concerned_VBN with_IN the_DT interactions_NNS between_IN computers_NNS and_CC human_JJ -LRB-_-LRB- natural_JJ -RRB-_-RRB- languages_NNS ._.
    ...

  • train_hmm()主要做了两件事：
    • 统计转移概率（transition probability），即连续的两个tag出现的频次/频率，对应HMM模型中的\(p(y_i|y_{i-1})\)。
    • 统计发射概率（emission probability），即某一个tag生成某一个word的频次/频率，对应HMM模型中的\(p(x_i|y_i)\)。

  • Demo 

    1
    $ python3 exercise/04-hmm/train_hmm.py --training-file='data/wiki-en-train.norm_pos' --model-file='exercise/04-hmm/my_model'

  • 输出文件（模型）： 

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    $ less exercise/04-hmm/my_model
    T DT NN 0.5120500782472613 # 以T开头的为转移概率
    T JJ NN 0.4236357765579593 # 表示上一个词性是JJ，则下一个词性是NN的概率为0.424。
    T IN DT 0.33908496732026144
    T NN IN 0.20562700964630226
    T . </s> 0.9785768936495792
    ...
    E NNP Learning 0.000727802037845706 # 以E开头的为发射概率
    E NN markup 0.0001607717041800643 # 表示从所有词性为NN的单词中选到markup的概率是0.00016。
    E NNP HTML 0.000727802037845706
    E NNS formats 0.0003832886163280951
    E NN PDF 0.0001607717041800643

HMM 随机采样

  • 初始化一个隐变量（词性），让马尔可夫链自动随机生成可观测变量（词）和下一个隐变量（词性），直至遇到EOS为止。

  • random_sample.py 该部分不再展示过多细节。核心函数numpy已经实现好了： 

    1
    2
    output_word = np.random.choice(candidate_word, p=candidate_word_prob)
    next_prob = np.random.choice(candidate_tag, p=candidate_tag_prob)

    第一行代码的意思是：（已知一个词性，）在一系列候选单词中，按照它们的分布概率（发射概率），随机选取一个单词作为可观测变量输出。

    第二行代码的意思类似：（已知前一个词性，）在一系列候选词性中，按照它门的分布（迁移概率），随机选取一个词性作为下一个词性输出。

  • Demo： 

    1
    $ python3 exercise/04-hmm/random_sample.py --model-file='exercise/04-hmm/my_model'

    多次重复可以得到不同的结果： 

    1
    2
    3
    4
    all the movie .
    how a words alone novel case is those gradual discourse or It is attaching This analyses .
    Journal 's Question Cynthia .
    simplest range segmentation scripts .

    注意，在我们观察输出的搞笑句子时，要想象这个句子由一个隐藏的词性链条在驱动着、生成着。

动态规划思想

  • 如果从最佳选择（最短、概率最大、负对数概率最小）的路径的末端截取一小部分，余下的路径仍然是最佳路径。

  • 特别关注一点：路径中的状态交点。

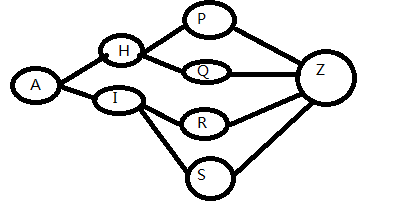
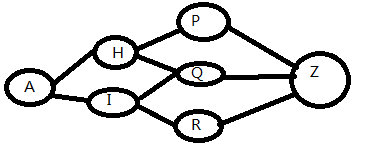
  • 动态规划可以解决任何一个图中的最短路径问题。

  • Q：怎么实现DP？ A：两种常用的方法。（仅仅涉及一般问题）
    • 自下而上：通过正向的loop，求出所有状态对应的值，然后找出max或者min。 优缺点：速度慢，但是相对节省空间。（本次实验展示的方法。）
    • 自上而下：通过递归的方法，需要求解\(f(x)\)，则必须知道\(f(y)\)，要知道\(f(y)\)，必须求\(f(z)\)。优缺点：速度快，只用算需要的值，但是要调用堆栈，浪费空间。（在这种思想中，动态规划实际上是对递归的优化（递归2.0），防止了不必要的递归（递归树中有相同分支））。

HMM 测试（维特比算法）

  • 维特比算法是一个特殊但应用最广的动态规划算法，专门针对一个特殊的图——篱笆网络（Lattice）有向图。凡使用HMM描述的问题都可以用它来解码。

  • 上图中，每一个单词下方都有一串候选词性（句子开始和结尾处的候选词性为<s>和</s>）。维特比算法中，
    • 前向部分，我们的任务是计算出从“初始状态节点（图中的0:<s>）”到每一步中每一个候选隐状态节点（图中的大量灰盒子，如2:NN）的最短路径和对应的概率值。
    • 反向部分，根据前面的结果得到一条完整的最佳路径。

  • 显然，在每两步之间（图中第\(i\)列和第\(i\)列）时，根据动态规划思想，我们已经知道、且无需再考虑之前第\(0\)列到第\(i-1\)列的最佳路径，直接拿来用即可。我们需要做的仅仅是采用两个for循环来对第\(i\)列和第\(i\)列的候选状态节点进行遍历即可。因此动态规划的复杂度为\(O(mn^2)\)（m是序列长度，n是每一层的候选隐状态个数）。

  • test_hmm.py的API和 main 函数： 

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    def load_model(model_file):  # 用于加载模型。
    def prob_trans(key, model):  # 用于从模型中返回转移概率。
    def prob_emiss(key, model):  # 用于从模型中返回发射概率。
    def forward(transition, emission, possible_tags, line):  # Viterbi算法的正向算法。
    def backward(best_edge, line):  # Viterbi算法的反向算法。
    def test_hmm(model_file, test_file, output_file):  # 总函数。
    if __name__ == '__main__':
        parser = argparse.ArgumentParser()  # 定义命令行传入参数。
        parser.add_argument('--model-file', type=str)
        parser.add_argument('--test-file', type=str)
        parser.add_argument('--output-file', type=str, default='stdout')
        args = parser.parse_args()
        test_hmm(args.model_file, args.test_file, args.output_file)

  • 前向算法（First Part）
    • 使用log是因为原来的概率值相乘，有的数值过小，限于计算机的精度，相乘容易造成下溢。
    • 下图中，best_score['1 NN']表示从初始节点（'0 <s>'）到该节点（‘1 NN’）的最优路线的值（负对数）。
    • best_edge['1 NN'] = '0 <s>'（图中没有显示）表示从初始节点（'0 <s>'）到该节点（‘1 NN’）的最优路线中前一个节点是'0 <s>'。
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    # First part, described in Neubig's slides p.38.
    for next in possible_tags.keys():
        for prev in [SOS]:
            prev_key = '{} {}'.format(0, prev)
            next_key = '{} {}'.format(1, next)
            trans_key = '{} {}'.format(prev, next)
            emiss_key = '{} {}'.format(next, words[0])
            if prev_key in best_score and trans_key in transition:
                score = best_score[prev_key] + \
                        -math.log2(prob_trans(trans_key, transition)) + \
                        -math.log2(prob_emiss(emiss_key, emission))
                if next_key not in best_score or best_score[next_key] > score:
                    best_score[next_key] = score
                    best_edge[next_key] = prev_key
  • 前向算法（Middle Part）
    • best_score['2 NN']表示从初始节点（'0 <s>'）到该节点（‘2 NN’）的最优路线的值（负对数）。因为要取最优，显然本层每个单元要对前一层的所有单元进行一次计算，然后取最小值。所以代码中有两个for循环。所以算法复杂度为O(nm^2)。
    • best_edge['2 NN'] = '1 JJ'（打个比方，图中没有显示）表示从初始节点（'0 <s>'）到该节点（‘2 NN’）的最优路线中前一个节点是'1 JJ'。
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    # Middle part, described in Neubig's slides p.39.
    for i in range(1, l):
        for next in possible_tags.keys():
            for prev in possible_tags.keys():
                prev_key = '{} {}'.format(i, prev)
                next_key = '{} {}'.format(i + 1, next)
                trans_key = '{} {}'.format(prev, next)
                emiss_key = '{} {}'.format(next, words[i])
                if prev_key in best_score and trans_key in transition:
                    score = best_score[prev_key] + \
                            -math.log2(prob_trans(trans_key, transition)) + \
                            -math.log2(prob_emiss(emiss_key, emission))
                    if next_key not in best_score or best_score[next_key] > score:
                        best_score[next_key] = score
                        best_edge[next_key] = prev_key

  • 前向算法（Final Part）

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    # Final part, described in Neubig's slides p.40.
    for next in [EOS]:
        for prev in possible_tags.keys():
            prev_key = '{} {}'.format(l, prev)
            next_key = '{} {}'.format(l + 1, next)
            trans_key = '{} {}'.format(prev, next)
            emiss_key = '{} {}'.format(next, EOS)
            if prev_key in best_score and trans_key in transition:
                score = best_score[prev_key] + \
                        -math.log2(prob_trans(trans_key, transition))
                if next_key not in best_score or best_score[next_key] > score:
                    best_score[next_key] = score
                    best_edge[next_key] = prev_key
  • 反向算法
    • 反向算法即按照前向函数forward()返回的best_edge，从尾到首走一遍即可。

  • Demo

    测试语料内容为： 

    1
    2
    3
    $ less data/wiki-en-test.norm
    In computational linguistics , word-sense disambiguation -LRB- WSD -RRB- is an open problem of natural language processing , which governs the process of identifying which sense of a word -LRB- i.e. meaning -RRB- is used in a sentence , when the word has multiple meanings -LRB- polysemy -RRB- .
    ...

    运行程序： 

    1
    $ python3 exercise/04-hmm/test_hmm.py --model-file='exercise/04-hmm/my_model' --test-file='data/wiki-en-test.norm' --output-file='exercise/04-hmm/my_answer.pos'

    一般这个程序会跑10s-20s左右。跑得结果： 

    1
    2
    3
    $ less exercise/04-hmm/my_answer.pos
    IN JJ NNS , DT NN -LRB- NN -RRB- VBZ DT JJ NN IN JJ NN NN , WDT VBZ DT NN IN VBG DT NN IN DT NN -LRB- FW NN -RRB- VBZ VBN IN DT NN , WRB DT NN VBZ JJ NNS -LRB- NN -RRB- .
    ...

  • 评测性能 

    1
    $ perl script/gradepos.pl data/wiki-en-test.pos exercise/04-hmm/my_answer.pos

    如果没错的话，你应该看到90.82%的正确率！ 

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    Accuracy: 90.82% (4144/4563)
    Most common mistakes:
    NNS --> NN	45
    NN --> JJ	27
    NNP --> NN	22
    JJ --> DT	22
    VBN --> NN	12
    JJ --> NN	12
    NN --> IN	11
    NN --> DT	10
    NNP --> JJ	8
    JJ --> VBN	7

参考文献

  1. Slides of 04-hmm of nlptutorial, by Graham Neubig
  2. Lecture Notes of Coursera: Natural Language Process, by Michael Collins
  3. 机器学习, 周志华 著
  4. 如何理解动态规划？, 知乎
  5. 数学之美, 吴军 著